深度学习第三章节
2025年11月17日大约 13 分钟
深度学习第三章节
1 PyTorch构建线性回归模型
1.1 创建数据集
import torch
from torch.utils.data import TensorDataset # 创建x和y张量数据集对象
from torch.utils.data import DataLoader # 创建数据集加载器
import torch.nn as nn # 损失函数和回归函数
from torch.optim import SGD # 随机梯度下降函数, 取一个训练样本算梯度值
from sklearn.datasets import make_regression # 创建随机样本, 工作中不使用
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# todo: 1-创建线性回归样本 x y coef(w) b
def create_datasets():
x, y, coef = make_regression(n_samples=100, # 样本数
n_features=1, # 特征数
noise=10, # 标准差, 噪声, 样本离散程度
coef=True, # 返回系数, w
bias=14.5, # 截距 b
random_state=0)
# 将数组转换成张量
x = torch.tensor(data=x)
y = torch.tensor(data=y)
# print('x->', x)
# print('y->', y)
# print('coef->', coef)
return x, y, coef
if __name__ == '__main__':
x, y, coef = create_datasets()1.2 训练模型
# todo: 2-模型训练
def train(x, y, coef):
# 创建张量数据集对象
datasets = TensorDataset(x, y)
print('datasets->', datasets)
# 创建数据加载器对象
# dataset: 张量数据集对象
# batch_size: 每个batch的样本数
# shuffle: 是否打乱样本
dataloader = DataLoader(dataset=datasets, batch_size=16, shuffle=True)
print('dataloader->', dataloader)
# for batch in dataloader: # 每次遍历取每个batch样本
# print('batch->', batch) # [x张量对象, y张量对象]
# break
# 创建初始回归模型对象, 随机生成w和b, 元素类型为float32
# in_features: 输入特征数 1个
# out_features: 输出特征数 1个
model = nn.Linear(in_features=1, out_features=1)
print('model->', model)
# 获取模型对象的w和b参数
print('model.weight->', model.weight)
print('model.bias->', model.bias)
print('model.parameters()->', list(model.parameters()))
# 创建损失函数对象, 计算损失值
criterion = nn.MSELoss()
# 创建SGD优化器对象, 更新w和b
optimizer = SGD(params=model.parameters(), lr=0.01)
# 定义变量, 接收训练次数, 损失值, 训练样本数
epochs = 100
loss_list = [] # 存储每次训练的平均损失值
total_loss = 0.0
train_samples = 0
for epoch in range(epochs): # 训练100次
# 借助循环实现 mini-batch SGD 模型训练
for train_x, train_y in dataloader:
# 模型预测
# train_x->float64
# w->float32
y_pred = model(train_x.type(dtype=torch.float32)) # y=w*x+b
print('y_pred->', y_pred)
# 计算损失值, 调用损失函数对象
# print('train_y->', train_y)
# y_pred: 二维张量
# train_y: 一维张量, 修改成二维张量, n行1列
# 可能发生报错, 修改形状
# 修改train_y元素类型, 和y_pred类型一致, 否则发生报错
loss = criterion(y_pred, train_y.reshape(shape=(-1, 1)).type(dtype=torch.float32))
print('loss->', loss)
# 获取loss标量张量的数值 item()
# 统计n次batch的总MSE值
total_loss += loss.item()
# 统计batch次数
train_samples += 1
# 梯度清零
optimizer.zero_grad()
# 计算梯度值
loss.backward()
# 梯度更新 w和b更新
# step()等同 w=w-lr*grad
optimizer.step()
# 每次训练的平均损失值保存到loss列表中
loss_list.append(total_loss / train_samples)
print('每次训练的平均损失值->', total_loss / train_samples)
print('loss_list->', loss_list)
print('w->', model.weight)
print('b->', model.bias)
# 绘制每次训练损失值曲线变化图
plt.plot(range(epochs), loss_list)
plt.title('损失值曲线变化图')
plt.grid()
plt.show()
# 绘制预测值和真实值对比图
# 绘制样本点分布
plt.scatter(x, y)
# 获取1000个样本点
# x = torch.linspace(start=x.min(), end=x.max(), steps=1000)
# 计算训练模型的预测值
y1 = torch.tensor(data=[v * model.weight + model.bias for v in x])
# 计算真实值
y2 = torch.tensor(data=[v * coef + 14.5 for v in x])
plt.plot(x, y1, label='训练')
plt.plot(x, y2, label='真实')
plt.legend()
plt.grid()
plt.show()
if __name__ == '__main__':
x, y, coef = create_datasets()
train(x, y, coef)2 人工神经网络介绍
2.1 什么是人工神经网络
- 仿生生物学神经网络的计算模型
- ANN(人工神经网络)->NN(神经网络)
2.2 如何构建人工神经网络
神经网络是由三个层, 每层由多个神经元构成
- 输入层: 输入样本的特征值, 一层
- 隐藏层: 提取复杂特征, 可以有多层
- 输出层: 输出y值, y预测值
2.3 人工神经网络内部状态值和激活值
神经元如何工作
- 内部状态值(加权求和值)
z=w1*x1+w2*x2+...+b
- 激活值
a=f(z)
3 激活函数介绍
3.1 激活函数作用
- 给神经网络模型中引入非线性因素
- 生产环境中,问题存在线性不可分情况
3.2 常见激活函数
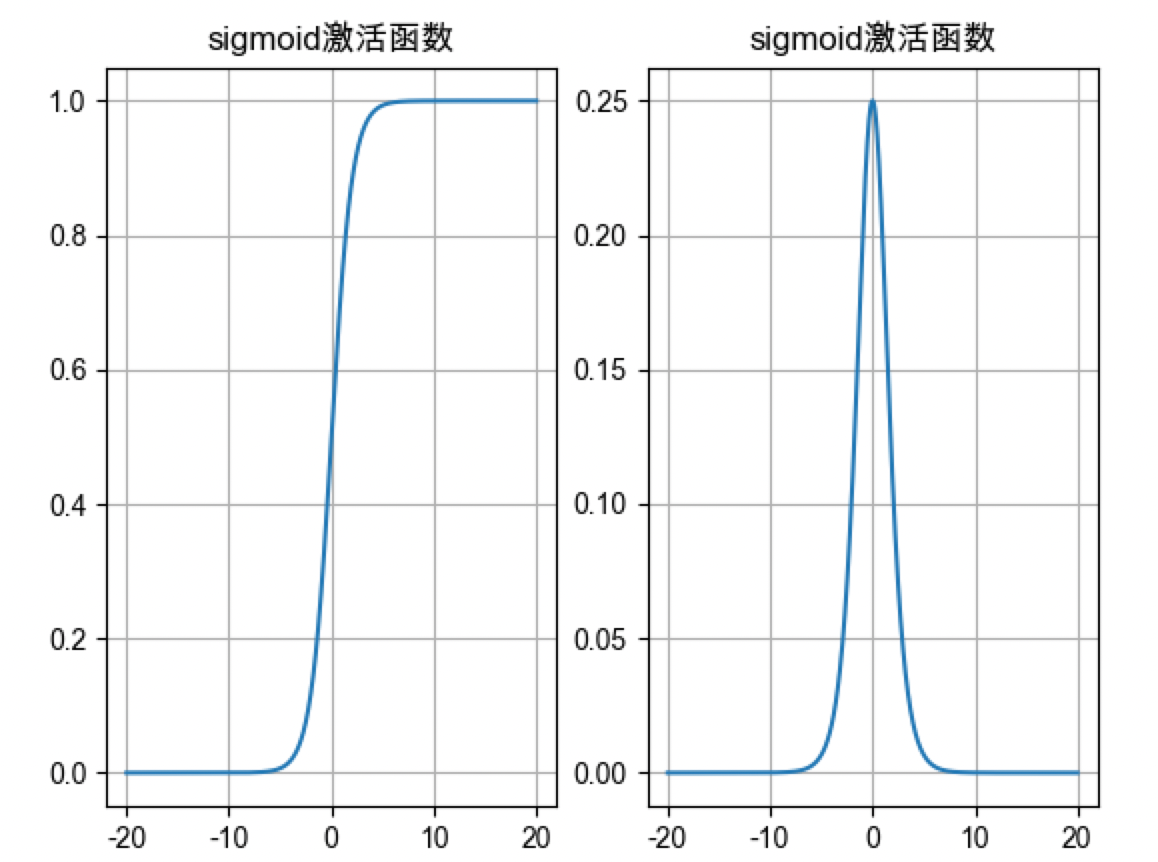
sigmoid激活函数
- sigmoid激活值范围是[0, 1], 只有正信号, 没有负信号, 模型只能学习到正信号
- 加权求和值在[-6,6]范围, 计算激活值时分布到[0, 1], 否则激活值只能是0或1
- sigmoid激活函数导数值范围是[0,0.25], 加权求和值在[-6,6]范围, 激活值梯度才分布到[0, 0.25], 否则梯度为0
- 神经网络中梯度连乘, sigmoid激活函数梯度值很小, 接近0, 梯度消失
0.25*0.25*0.25*... - sigmoid一般在二分类输出层使用, 如果神经网络隐藏层在5层之内也可以考虑使用sigmoid,实践中使用很少
# sigmoid激活值: torch.sigmoid(x) import torch import matplotlib.pyplot as plt plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 def dm01(): # 创建x值, 线性模型输出值作为激活函数的输入值 x = torch.linspace(-20, 20, 1000) # 计算激活值 y = torch.sigmoid(input=x) # 创建画布对象和坐标轴对象 _, axes = plt.subplots(1, 2) # 一行两列, 绘制两个子图 axes[0].plot(x, y) axes[0].grid() axes[0].set_title('sigmoid激活函数') # 创建x值,可以自动微分, 线性模型输出值作为激活函数的输入值 x = torch.linspace(-20, 20, 1000, requires_grad=True) torch.sigmoid(input=x).sum().backward() axes[1].plot(x.detach().numpy(), x.grad) axes[1].grid() axes[1].set_title('sigmoid激活函数') plt.show() if __name__ == '__main__': dm01()
tanh激活函数
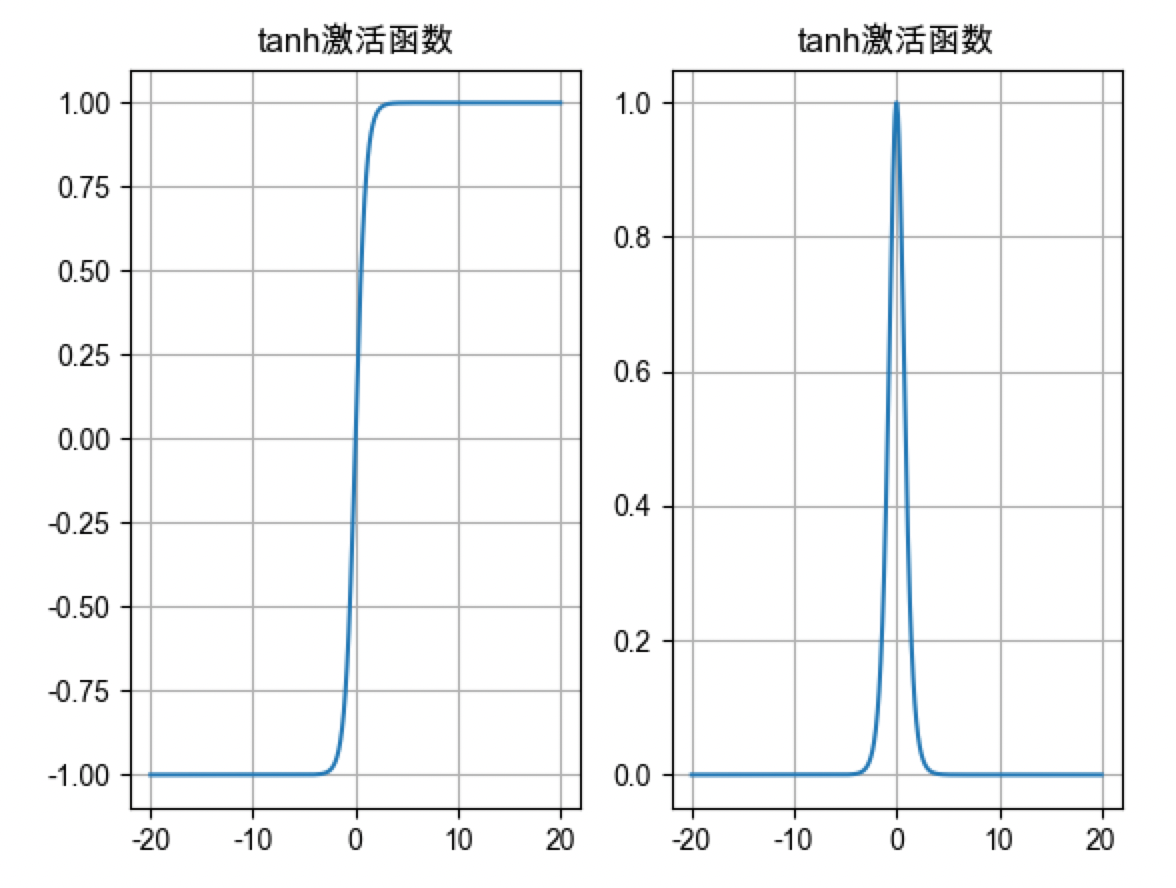
- tanh激活值范围是[-1, 1], 既有正信号, 又有负信号, 激活值是以0对称, 模型可以学习到正负信号
- 加权求和值在[-3,3]范围, 计算激活值时分布到[-1, 1], 否则激活值只能是-1或1
- tanh激活函数导数值范围是[0,1], 加权求和值在[-3,3]范围, 相比sigmoid激活导数更大, 模型收敛程度更快, 迭代次数更少, 但是如果加权求和值大于3或小于-3, 也是会导致梯度消失, 最好分布在0附近(梯度值最大)
- tanh激活函数可以在隐藏层使用, 不是优先选择, 浅层神经网络可以使用
- 主要用于隐藏层(浅层不超过5层,因为深层使用tanh会导致梯度消失), 输出层使用sigmoid激活函数
# tanh激活值: torch.tanh(x) import torch import matplotlib.pyplot as plt from torch.nn import functional as F # F.sigmoid() # F.tanh() plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 def dm01(): # 创建x值, 线性模型输出值作为激活函数的输入值 x = torch.linspace(-20, 20, 1000) # 计算激活值 y = torch.tanh(input=x) # 创建画布对象和坐标轴对象 _, axes = plt.subplots(1, 2) # 一行两列, 绘制两个子图 axes[0].plot(x, y) axes[0].grid() axes[0].set_title('tanh激活函数') # 创建x值,可以自动微分, 线性模型输出值作为激活函数的输入值 x = torch.linspace(-20, 20, 1000, requires_grad=True) torch.tanh(input=x).sum().backward() axes[1].plot(x.detach().numpy(), x.grad) axes[1].grid() axes[1].set_title('tanh激活函数') plt.show() if __name__ == '__main__': dm01()
relu激活函数
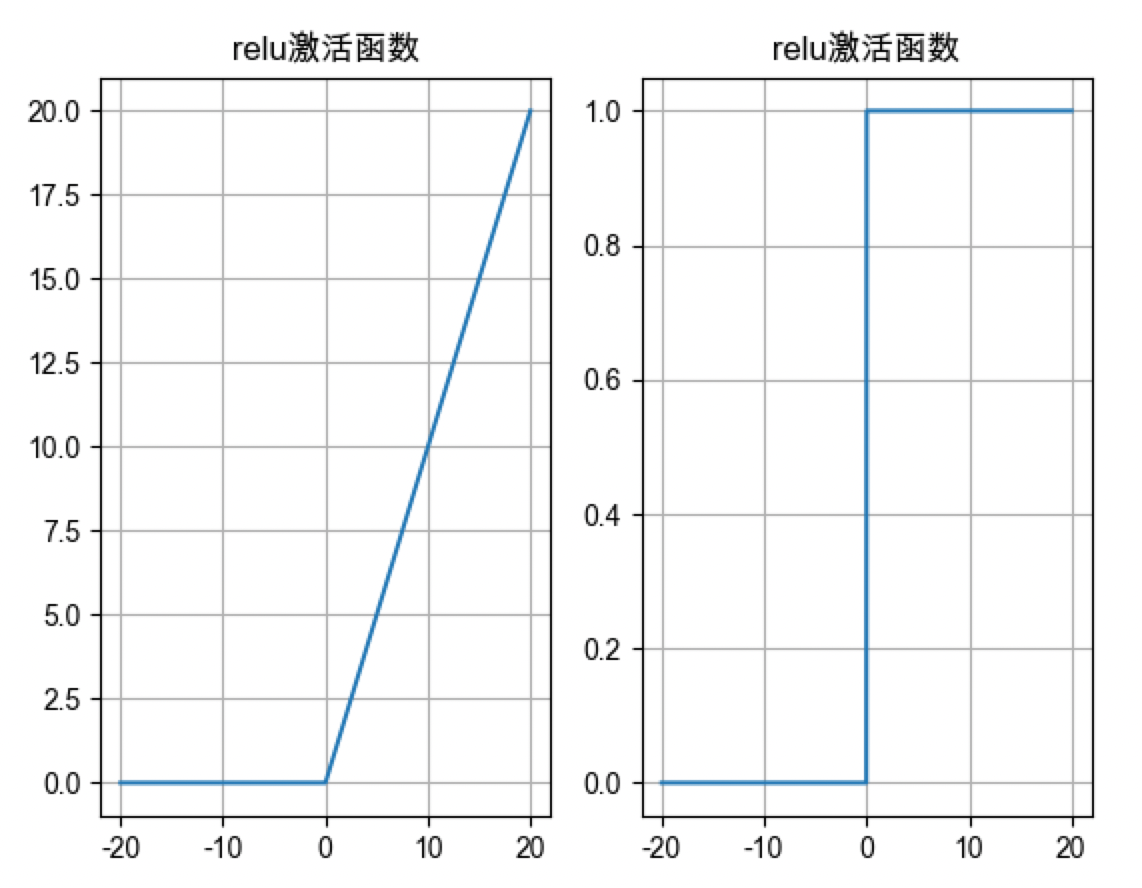
- relu激活值范围是[0, x], x是线性输出的正值, 只有正信号
- 加权求和值大于0, 也可以一部分小于0(神经元死亡, 防止过拟合)
- relu激活函数导数值0或1, 如果线性输出大于0, 导数为1, 不会出现梯度消失情况, 模型收敛程度更快, 比tanh收敛程度更快; 如果线性输出小于0, 权重不更新这个现象称为神经元死亡, 防止过拟合(选择leaky relu或prelu)
- relu激活函数优先选择, 计算复杂度最小, 大于0不存在梯度消失情况
- 适合隐藏层,深层因为没有梯度消失问题
# relu激活值: torch.relu(x) import torch import matplotlib.pyplot as plt from torch.nn import functional as F # F.sigmoid() # F.tanh() plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 def dm01(): # 创建x值, 线性模型输出值作为激活函数的输入值 x = torch.linspace(-20, 20, 1000) # 计算激活值 y = torch.relu(input=x) # torch.leaky_relu() # torch.prelu() # 创建画布对象和坐标轴对象 _, axes = plt.subplots(1, 2) # 一行两列, 绘制两个子图 axes[0].plot(x, y) axes[0].grid() axes[0].set_title('relu激活函数') # 创建x值,可以自动微分, 线性模型输出值作为激活函数的输入值 x = torch.linspace(-20, 20, 1000, requires_grad=True) torch.relu(input=x).sum().backward() axes[1].plot(x.detach().numpy(), x.grad) axes[1].grid() axes[1].set_title('relu激活函数') plt.show() if __name__ == '__main__': dm01()
softmax激活函数
- 多分类任务的输出层使用, 将输出层加权求和值转换成概率
- 比如a,b,c,d,e,f,g,h,i,j 10个类别, 输出层加权求和值为[0.2, 0.02, 0.15, 0.15, 1.3, 0.5, 0.06, 1.1, 0.05, 3.75], 通过softmax激活函数转换成概率值为[0.018, 0.002, 0.013, 0.013, 0.118, 0.046, 0.006, 0.099, 0.005, 0.331]
- 概率值之和为1
- 概率值最大的为3.75, 对应的类别为j
- 概率值最小的为0.002, 对应的类别为b
- 概率值中间的为0.046, 对应的类别为f
import torch import pandas as pd def dm01(): # 创建输出层加权求和值 y = torch.tensor(data=[[0.2, 0.02, 0.15, 0.15, 1.3, 0.5, 0.06, 1.1, 0.05, 3.75], [0.2, 0.02, 0.15, 3.75, 1.3, 0.5, 0.06, 1.1, 0.05, 0.15]]) # softmax激活函数转换成概率值 # 1轴按列计算 # y_softmax = torch.softmax(input=y, dim=-1) y_softmax = torch.softmax(input=y, dim=1) print('y_softmax->', y_softmax) if __name__ == '__main__': dm01()
3.6 如何选择激活函数
隐藏层
- 优选relu激活函数, 其次选leaky relu/prelu > tanh > sigmoid
- 尽量少使用sigmoid激活函数, 可以使用tanh激活函数代替sigmoid激活函数 浅层神经网络
输出层
- 二分类问题 sigmoid激活函数
- 多分类问题 softmax激活函数
- 回归问题 identity激活函数
激活函数总结
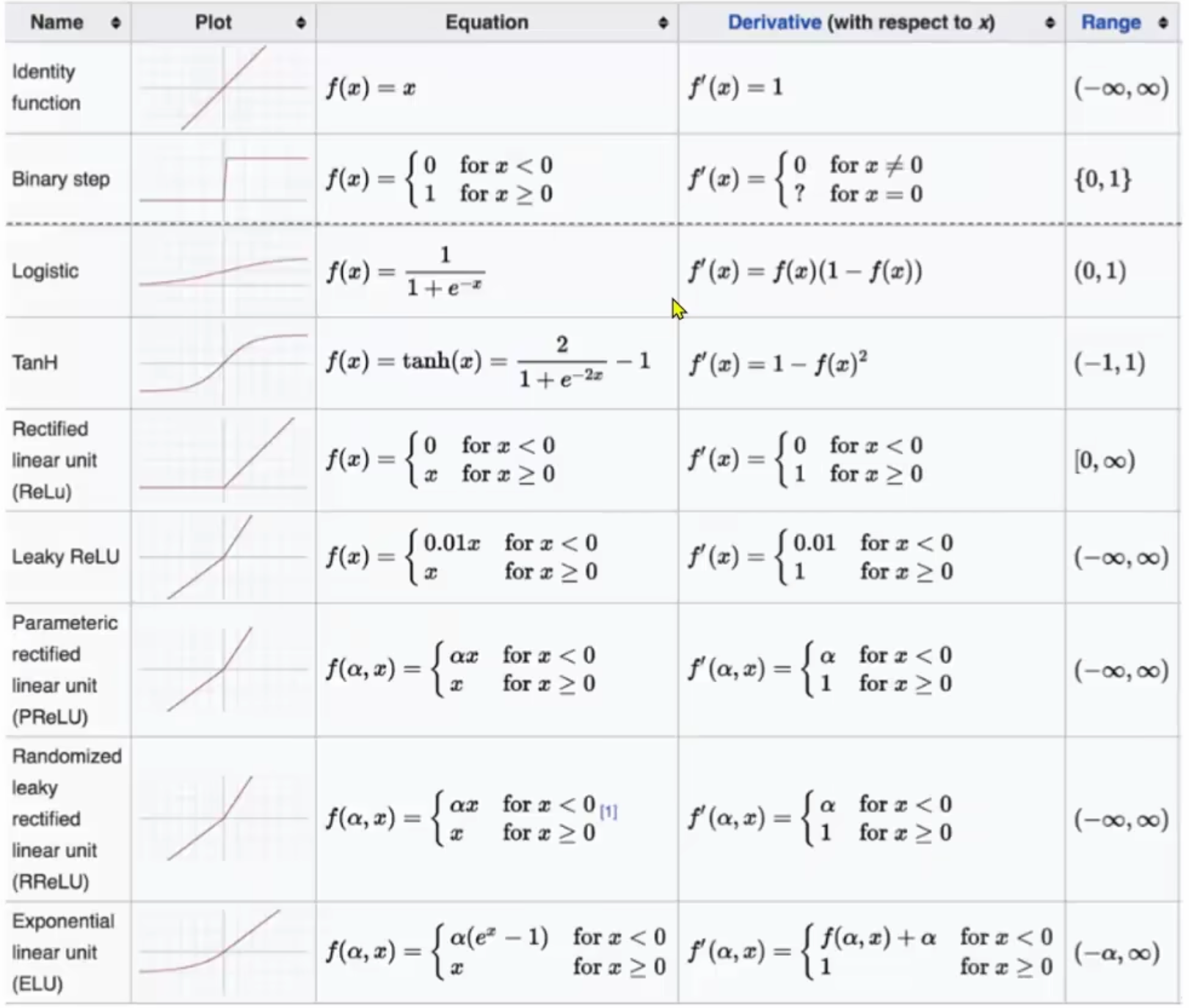
- 激活函数的作用是引入非线性因素, 增加模型复杂度, 提高模型表达能力
- 神经网络绝大多数是处理分类问题, 只有少部分是处理回归问题
4 参数初始化
- 参数初始化的目的:
- 防止梯度消失
- 防止梯度爆炸
- 加快模型收敛速度
- 打破对称性
4.1 参数初始化作用
- 参数->w和b, 创建初版模型时指定w和b的值
- 选择合适的参数, 计算得到的加权求和的值会落到激活函数合理的区间, 加快模型收敛速度以及增加不同学习特征值
4.2 常见参数初始化方法
1. 随机初始化
- 优点:避免神经元输出一致导致的梯度消失,实现简单。
- 缺点:随机范围难把控,过大易导致激活值饱和,过小则梯度微弱。
- 使用场景:适用于简单模型或无明确适配初始化的场景,需配合合适的随机范围(如[-0.01, 0.01])。
2. 全0/1初始化
- 优点:实现极简,参数完全一致。
- 缺点:全0会导致所有神经元输出相同,梯度更新同步失效;全1易使激活值饱和,梯度消失。
- 使用场景:仅适用于偏置项(bias)初始化(全0为主),绝对不能用于权重初始化。
3. 固定值初始化
- 优点:参数可控,结果可复现,实现简单。
- 缺点:固定值易导致神经元功能同质化,复杂模型中梯度传播受阻。
- 使用场景:简单线性模型、调试阶段验证代码,或对参数有明确先验知识的场景。
4. Kaiming初始化
- 优点:专为ReLU及其变种(如Leaky ReLU)设计,适配其非对称激活特性,有效缓解梯度消失/爆炸。
- 缺点:不适用于Sigmoid、Tanh等对称激活函数,会导致输出方差失衡。
- 使用场景:采用ReLU系列激活函数的模型,如CNN、ResNet、Transformer的部分层。
5. Xavier初始化
- 优点:适配Sigmoid、Tanh等对称激活函数,保证前向传播输出方差与反向传播梯度方差一致。
- 缺点:用于ReLU时效果不佳,无法抵消ReLU对负数部分的“截断”影响。
- 使用场景:采用Sigmoid、Tanh激活函数的模型,如传统DNN、RNN的隐藏层。
4.3 权重初始化方法速查表
| 初始化方法 | 核心公式(简化版) | 适用激活函数 | 核心代码示例(PyTorch) |
|---|---|---|---|
| 随机初始化 | 权重 ~ Uniform(-a, a)(a通常取0.01)或 Normal(0, σ²)(σ取0.01) | 通用(无明确适配时) | nn.init.uniform_(w, -0.01, 0.01) 或 nn.init.normal_(w, 0, 0.01) |
| 全0/1初始化 | 权重 = 0 或 权重 = 1 | 仅偏置项(全0) | nn.init.zeros_(bias) (权重禁用全0/1) |
| 固定值初始化 | 权重 = 预设固定值(如0.02、0.1) | 简单线性模型、调试场景 | nn.init.constant_(w, 0.02) |
| Kaiming初始化 | 均匀分布:w ~ Uniform(-√(6/(fan_in)), √(6/(fan_in)));正态分布:w ~ Normal(0, √(2/fan_in)) | ReLU、Leaky ReLU、GELU等 | nn.init.kaiming_uniform_(w, mode='fan_in', nonlinearity='relu') |
| Xavier初始化 | 均匀分布:w ~ Uniform(-√(6/(fan_in+fan_out)), √(6/(fan_in+fan_out)));正态分布:w ~ Normal(0, √(2/(fan_in+fan_out))) | Sigmoid、Tanh、Softmax | nn.init.xavier_uniform_(w, gain=nn.init.calculate_gain('tanh')) |
import torch
import torch.nn as nn
# 随机参数初始化
def dm01():
# 创建线性层对象, 对线性层的权重进行初始化
# in_features: 输入神经元个数
# out_features: 输出神经元个数
linear1 = nn.Linear(in_features=5, out_features=8)
linear2 = nn.Linear(in_features=8, out_features=10)
# 均匀分布初始化,默认在(0,1)区间均匀分布, 可以通过a和b参数调整区间
nn.init.uniform_(linear1.weight)
nn.init.uniform_(linear1.weight, a=-1/torch.sqrt(torch.tensor(5.0)), b=1/torch.sqrt(torch.tensor(5.0)))
nn.init.uniform_(linear1.bias)
print(linear1.weight)
print(linear1.bias)
# 正态分布参数初始化
def dm02():
# 创建线性层对象, 对线性层的权重进行初始化
# in_features: 输入神经元个数
# out_features: 输出神经元个数
linear1 = nn.Linear(in_features=5, out_features=8)
linear2 = nn.Linear(in_features=8, out_features=10)
# 均匀分布初始化
nn.init.normal_(linear1.weight)
nn.init.normal_(linear1.bias)
print(linear1.weight)
print(linear1.bias)
# nn.init.zeros_() # 全0初始化
# nn.init.ones_() # 全1初始化
# nn.init.constant_(val=0.1) # 全固定值初始化
# nn.init.kaiming_uniform_() # 凯明均匀分布初始化
# nn.init.kaiming_normal_() # 凯明正态分布初始化
# nn.init.xavier_uniform_() # xavier均匀分布初始化
# nn.init.xavier_normal_() # xavier正态分布初始化
if __name__ == '__main__':
dm01()
dm02()4.3 如何选择参数初始化方法
- 浅层神经网络可以选择随机初始化
- 深层神经网络结合激活函数选择
- tanh激活函数 -> xavier初始化
- relu激活函数 -> kaiming初始化
4.4 参数初始化总结
参数初始化的目的
- 防止梯度消失或梯度爆炸
- 提高收敛速度
- 打破对称性
参数初始化的方式
无法打破对称性的
- 全0初始化
- 全1初始化
- 固定值初始化
可以打破对称性的
- 随机初始化
- 正态分布初始化
- kaiming初始化
- xavier初始化
总结
- 重点记忆:kaiming初始化、xavier初始化、全0初始化
- 初始化选择原则:
- 激活函数为ReLU及其系列:优先使用kaiming初始化
- 激活函数为非ReLU(如Sigmoid、Tanh):优先使用xavier初始化
- 浅层网络:可考虑使用随机初始化
