数据结构
数据结构
数据结构的概念
基本概念
- 数据:能输入到计算机中并且被计算机程序处理的符号的总称
- 数据元素:数据的基本单位。有时,一个数据元素可由若干数据项组成
- 数据结构的存储方式:
- 顺序存储:把逻辑上相邻的结点存储在物理位置上相邻的存储单元中
- 链式存储:把逻辑上相邻的结点存储在物理位置上不相邻的存储单元中,结点间的逻辑关系是由附加的指针字段表示的
- 索引存储:存储结点信息的同时,还建立附加的索引表,索引表中的每一项称为索引项,索引项的一般形式是(关键字,地址)
- 散列存储:根据结点的关键字直接计算出该结点的存储地址
- 算法:
- 算法特征:有穷性、确切性、输入、输出、可行性
- 算法评定:健壮性、可读性、正确性、空间复杂度
- 时间复杂度:算法运行时间随问题规模增长的变化趋势
- 空间复杂度:算法运行时所占用的存储空间随问题规模增长的变化趋势
线性表
- 线性表的表示方法:顺序表示、链式表示。
- 线性表的存储结构和实现:线性链表、循环链表、双向链表。
- 链表的四种形式:单链表、双链表、循环单链表、循环双链表。
- 线性表的相关操作
- 线性链表判空(L 为头指针):
带头结点:L→next==null;
不带头结点:L==null
循环链表判空:L→next==L
双向链表判空:L→next==L顺序表和链表的比较
| 对比维度 | 顺序表 | 链表 |
|---|---|---|
| 存储结构 | 顺序存储(数组) | 链式存储(指针连接结点) |
| 存取方式 | 支持顺序 + 随机访问 | 只能从表头顺序访问(逐个遍历) |
| 按序号查找 | O(1)(直接通过下标访问) | O(n)(逐个结点向后找) |
| 按值查找 | 无序:O(n);有序可二分:O(log n) | O(n) |
| 插入操作 | 平均需移动半个表长元素,O(n) | 修改指针即可,O(1)(找到位置后) |
| 删除操作 | 同插入,平均 O(n) | 修改指针即可,O(1)(找到位置后) |
| 存储密度 | 高(只存值) | 低(每个结点需额外指针域) |
| 空间分配 | 需预分配固定大小(可能浪费) | 动态分配,灵活但碎片化 |
| 扩容方式 | 需手动申请更大数组并复制元素 | 不需要,动态申请新结点 |
| 应用场景 | 查询频繁、数据量稳定 | 插入/删除频繁、不定长数据 |
- 顺序表中插入元素,平均要移动的元素个数为:n/2
- 在一个长度为n的顺序表中,在第i个元素(1≤i≤n+1)之前插入一个新元素时须向后移动n-i+1个元素
栈和队列
- 栈和队列的定义
- 栈:栈是限定仅在表尾进行插入或删除操作的线性表。先进后出,后进先出
- 队列:队列是只允许在一端进行插入操作、而在另一端进行删除操作的线性表。先进先出,后进后出
栈
- 应用:
- 数制转换:将一个数从一种进制转换为另一种进制
- 括号匹配检验:检查表达式中的括号是否匹配
- 行编辑程序:编辑程序中的行编辑功能
- 表达式求值:将中缀表达式转换为后缀表达式,然后求值
- 操作:
- 判空:S.top == -1
- 判满:S.top == MaxSize - 1
- 进栈要先移动指针,再进元素
- 出栈要先取元素,再移动指针
队列
- 应用:
- 层次遍历
- 比如二叉树的层次遍历
- 计算机系统
- 解决主机与外部设备之间速度不匹配
- 解决由多用户引起的资源竞争
- 层次遍历
- 操作:
- 判空:Q.front == Q.rear
- 判满:(rear+1)mod MAXSIZE==front
- 求元素个数:(rear-front+MAXSIZE)mod MAXSIZE
- 插入:(rear+n)mod MAXSIZE
- 删除:(front+n)mod MAXSIZE
循环队列
队空的条件:Q.front == Q.rear
解释:当队头指针与队尾指针指向同一位置时,队列中没有元素(初始状态或所有元素出队后均满足)。队满的条件:(Q.rear + 1) % MAXQSIZE == Q.front
解释:预留一个空位置作为标记,当队尾指针后移一位(循环后)与队头指针重合时,队列已满(避免与队空条件冲突)。入队:Q.rear = (Q.rear + 1) % MAXQSIZE
解释:元素入队后,队尾指针后移一位,若超出数组长度则通过取模回到起点,形成环形。出队:Q.front = (Q.front + 1) % MAXQSIZE
解释:元素出队后,队头指针后移一位,同样通过取模实现环形移动,指向新的队头元素。当前元素个数:(Q.rear - Q.front + MAXQSIZE) % MAXQSIZE
解释:通过队尾与队头指针的差值计算元素数,加MAXQSIZE再取模是为了避免 rear < front 时出现负数(确保结果为正数)。
举例:
1. 栈的操作举例(MaxSize = 5)
初始状态:
S.top = -1
S.data = [ ][ ][ ][ ][ ]
判空:S.top == -1 ✓(栈为空)
判满:S.top == MaxSize - 1 = 4(当前不满足,所以栈未满)操作1:进栈操作(先移动指针,再进元素)
1. 进栈 'A':
- 先移动指针:S.top = S.top + 1 = 0
- 再进元素:S.data[0] = 'A'
状态:S.top = 0, S.data = [A][ ][ ][ ][ ]
判空:S.top == -1 ✗(不满足,所以栈不为空)
判满:S.top == 4 ✗(不满足,所以栈未满)
2. 进栈 'B':
- 先移动指针:S.top = 1
- 再进元素:S.data[1] = 'B'
状态:S.top = 1, S.data = [A][B][ ][ ][ ]
3. 进栈 'C':
- 先移动指针:S.top = 2
- 再进元素:S.data[2] = 'C'
状态:S.top = 2, S.data = [A][B][C][ ][ ]
4. 进栈 'D':
- 先移动指针:S.top = 3
- 再进元素:S.data[3] = 'D'
状态:S.top = 3, S.data = [A][B][C][D][ ]
5. 进栈 'E':
- 先移动指针:S.top = 4
- 再进元素:S.data[4] = 'E'
状态:S.top = 4, S.data = [A][B][C][D][E]
判满:S.top == 4 ✓(栈已满,不能再进栈)操作2:出栈操作(先取元素,再移动指针)
1. 出栈:
- 先取元素:x = S.data[S.top] = S.data[4] = 'E'
- 再移动指针:S.top = S.top - 1 = 3
状态:S.top = 3, S.data = [A][B][C][D][E](E已取出)
返回值:'E'
2. 出栈:
- 先取元素:x = S.data[3] = 'D'
- 再移动指针:S.top = 2
状态:S.top = 2, S.data = [A][B][C][D][E]
返回值:'D'
3. 出栈:
- 先取元素:x = S.data[2] = 'C'
- 再移动指针:S.top = 1
状态:S.top = 1, S.data = [A][B][C][D][E]
返回值:'C'
4. 出栈:
- 先取元素:x = S.data[1] = 'B'
- 再移动指针:S.top = 0
状态:S.top = 0, S.data = [A][B][C][D][E]
返回值:'B'
5. 出栈:
- 先取元素:x = S.data[0] = 'A'
- 再移动指针:S.top = -1
状态:S.top = -1, S.data = [A][B][C][D][E]
判空:S.top == -1 ✓(栈为空,不能再出栈)
返回值:'A'2. 队列的操作举例(MAXSIZE = 5)
初始状态:
Q.front = 0
Q.rear = 0
Q.data = [ ][ ][ ][ ][ ]
判空:Q.front == Q.rear ✓(队列为空)
判满:(rear+1) mod MAXSIZE == front → (0+1) mod 5 = 1 ≠ 0 ✗(队列未满)
元素个数:(rear-front+MAXSIZE) mod MAXSIZE = (0-0+5) mod 5 = 0操作1:插入操作(入队)
1. 插入 'A':
- rear = (rear + 1) mod MAXSIZE = (0 + 1) mod 5 = 1
- Q.data[rear] = Q.data[1] = 'A'(实际存储位置)
状态:front = 0, rear = 1, Q.data = [ ][A][ ][ ][ ]
判空:front == rear → 0 == 1 ✗(队列不为空)
判满:(rear+1) mod MAXSIZE == front → (1+1) mod 5 = 2 ≠ 0 ✗
元素个数:(1-0+5) mod 5 = 1
2. 插入 'B':
- rear = (1 + 1) mod 5 = 2
- Q.data[2] = 'B'
状态:front = 0, rear = 2, Q.data = [ ][A][B][ ][ ]
元素个数:(2-0+5) mod 5 = 2
3. 插入 'C':
- rear = (2 + 1) mod 5 = 3
- Q.data[3] = 'C'
状态:front = 0, rear = 3, Q.data = [ ][A][B][C][ ]
元素个数:(3-0+5) mod 5 = 3
4. 插入 'D':
- rear = (3 + 1) mod 5 = 4
- Q.data[4] = 'D'
状态:front = 0, rear = 4, Q.data = [ ][A][B][C][D]
判满:(rear+1) mod MAXSIZE == front → (4+1) mod 5 = 0 == 0 ✓(队列已满)
元素个数:(4-0+5) mod 5 = 4操作2:删除操作(出队)
1. 删除:
- 先取元素:x = Q.data[front] = Q.data[0] = 'A'
- front = (front + 1) mod MAXSIZE = (0 + 1) mod 5 = 1
状态:front = 1, rear = 4, Q.data = [ ][A][B][C][D]
返回值:'A'
判空:front == rear → 1 == 4 ✗(队列不为空)
元素个数:(4-1+5) mod 5 = 3
2. 删除:
- x = Q.data[1] = 'B'
- front = (1 + 1) mod 5 = 2
状态:front = 2, rear = 4, Q.data = [ ][A][B][C][D]
返回值:'B'
元素个数:(4-2+5) mod 5 = 2
3. 删除:
- x = Q.data[2] = 'C'
- front = (2 + 1) mod 5 = 3
状态:front = 3, rear = 4, Q.data = [ ][A][B][C][D]
返回值:'C'
元素个数:(4-3+5) mod 5 = 1
4. 删除:
- x = Q.data[3] = 'D'
- front = (3 + 1) mod 5 = 4
状态:front = 4, rear = 4, Q.data = [ ][A][B][C][D]
返回值:'D'
判空:front == rear → 4 == 4 ✓(队列为空,不能再删除)
元素个数:(4-4+5) mod 5 = 03. 循环队列的操作举例(MAXQSIZE = 5)
初始状态:
Q.front = 0
Q.rear = 0
Q.data = [ ][ ][ ][ ][ ]
队空:Q.front == Q.rear → 0 == 0 ✓(队列为空)
队满:(Q.rear + 1) % MAXQSIZE == Q.front → (0+1) % 5 = 1 ≠ 0 ✗
元素个数:(Q.rear - Q.front + MAXQSIZE) % MAXQSIZE = (0-0+5) % 5 = 0操作序列:A入队 → B入队 → C入队 → A出队 → D入队 → E入队 → B出队 → F入队
步骤1:A入队
入队操作:Q.rear = (Q.rear + 1) % MAXQSIZE = (0 + 1) % 5 = 1
存储元素:Q.data[0] = 'A'(注意:rear指向下一个空位置,元素存在rear-1位置)
状态:front = 0, rear = 1
队列:[A][ ][ ][ ][ ]
↑front ↑rear
队空:0 == 1 ✗
队满:(1+1) % 5 = 2 ≠ 0 ✗
元素个数:(1-0+5) % 5 = 1步骤2:B入队
入队操作:Q.rear = (1 + 1) % 5 = 2
存储元素:Q.data[1] = 'B'
状态:front = 0, rear = 2
队列:[A][B][ ][ ][ ]
↑front ↑rear
元素个数:(2-0+5) % 5 = 2步骤3:C入队
入队操作:Q.rear = (2 + 1) % 5 = 3
存储元素:Q.data[2] = 'C'
状态:front = 0, rear = 3
队列:[A][B][C][ ][ ]
↑front ↑rear
元素个数:(3-0+5) % 5 = 3步骤4:A出队
出队操作:Q.front = (Q.front + 1) % MAXQSIZE = (0 + 1) % 5 = 1
取出元素:Q.data[0] = 'A'
状态:front = 1, rear = 3
队列:[ ][B][C][ ][ ]
↑front ↑rear
队空:1 == 3 ✗
元素个数:(3-1+5) % 5 = 2步骤5:D入队
入队操作:Q.rear = (3 + 1) % 5 = 4
存储元素:Q.data[3] = 'D'
状态:front = 1, rear = 4
队列:[ ][B][C][D][ ]
↑front ↑rear
元素个数:(4-1+5) % 5 = 3步骤6:E入队(循环到起点)
入队操作:Q.rear = (4 + 1) % 5 = 0(循环回到起点)
存储元素:Q.data[4] = 'E'
状态:front = 1, rear = 0(rear < front,已循环)
队列:[E][B][C][D][ ]
↑rear ↑front
队满:(0+1) % 5 = 1 == 1 ✓(队列已满,不能再入队)
元素个数:(0-1+5) % 5 = 4步骤7:B出队
出队操作:Q.front = (1 + 1) % 5 = 2
取出元素:Q.data[1] = 'B'
状态:front = 2, rear = 0
队列:[E][ ][C][D][ ]
↑rear ↑front
队空:2 == 0 ✗
队满:(0+1) % 5 = 1 ≠ 2 ✗(队列未满,可以入队)
元素个数:(0-2+5) % 5 = 3步骤8:F入队
入队操作:Q.rear = (0 + 1) % 5 = 1
存储元素:Q.data[0] = 'F'
状态:front = 2, rear = 1
队列:[E][F][C][D][ ]
↑rear ↑front
队满:(1+1) % 5 = 2 == 2 ✓(队列再次满)
元素个数:(1-2+5) % 5 = 4边界情况说明:
情况1:rear < front(循环后)
MAXQSIZE = 5, front = 3, rear = 1
队列:[X][X][ ][X][X]
↑rear ↑front
队空:3 == 1 ✗
队满:(1+1) % 5 = 2 ≠ 3 ✗
元素个数:(1-3+5) % 5 = 3
说明:rear绕了一圈后小于front,通过加MAXQSIZE再取模得到正确元素个数情况2:rear > front(正常情况)
MAXQSIZE = 5, front = 1, rear = 4
队列:[ ][X][X][X][ ]
↑front ↑rear
队空:1 == 4 ✗
队满:(4+1) % 5 = 0 ≠ 1 ✗
元素个数:(4-1+5) % 5 = 3
说明:正常情况,rear在front之后数组与特殊矩阵
数组:有序的元素序列
一维:LOC(ai)=LOC(a0)+i*L (0≤i<n)
这个公式描述的是线性地址分配中,第
i个元素的存储地址计算方式,常见于数组等连续存储的数据结构中。LOC(ai):表示第i个元素(如数组的第i个元素)在内存中的存储地址。LOC(a0):表示第一个元素(索引为 0 的元素)的起始地址(基地址)。i:元素的索引(从 0 开始,0≤i<n表示索引范围在 0 到n-1之间,共n个元素)。L:单个元素占用的内存空间大小(单位:字节,由元素类型决定,如 int 型通常为 4 字节)。
整体含义:第
i个元素的地址 = 首个元素的地址 + 索引i× 单个元素的大小。这体现了连续存储的特性——通过基地址和偏移量(i×L)可直接计算任意元素的地址,实现随机访问(时间复杂度 O(1))。二维数组在内存中其实是一维的。有两种存储方式:
- 行为主序:按行依次存储,先存完第 0 行,再存第 1 行,依此类推
- LOC(a[i][j]) = LOC(a[0][0]) + (i * 列数 + j) * L
- 举例:假设有一个 3行4列 的int数组(int arr[3][4]),基地址LOC(a[0][0])=2000,int占 4 字节(L=4)。
- 元素a[0][0]的地址:2000 + (0 * 3 + 0) * 4 = 2000
- 元素a[0][1]的地址:2000 + (0 * 3 + 1) * 4 = 2004
- 元素a[1][0]的地址:2000 + (1 * 3 + 0) * 4 = 2016(第 1 行前有 4 个元素,每个占 4 字节,共 16 字节)
- 元素a[2][3]的地址:2000 + (2 * 3 + 3) * 4 = 2000 + 11 * 4 = 2044
- 列为主序:按列依次存储,先存完第 0 列,再存第 1 列,依此类推
- LOC(a[i][j]) = LOC(a[0][0]) + (j * 行数 + i) * L
- 举例:假设有一个 3行4列 的int数组(int arr[3][4]),基地址LOC(a[0][0])=2000,int占 4 字节(L=4)。
- 元素a[0][0]的地址:2000 + (0 * 3 + 0) * 4 = 2000
- 元素a[1][0]的地址:2000 + (0 * 3 + 1) * 4 = 2004(第 0 列前有 1 个元素,每个占 4 字节)
- 元素a[0][1]的地址:2000 + (1 * 3 + 0) * 4 = 2012(第 1 列前有 3 个元素,共 12 字节)
- 元素a[2][3]的地址:2000 + (3 * 3 + 2) * 4 = 2000 + 11 * 4 = 2044
- 行为主序:按行依次存储,先存完第 0 行,再存第 1 行,依此类推
相关信息
- LOC(a[i][j]):第i行第j列元素的地址
- LOC(a[0][0]):数组基地址(第一个元素a[0][0]的地址)
- i:行下标
- j:列下标
- L:每个元素的内存单元数
- 多维数组是特殊的线性表,是线性表的推广
广义表
- 广义表的长度(广度)指:广义表中所包含的数据元素的个数,比如(a,b,c,d)的长度为4
- 广义表的深度指:广义表中所包含括号的重数,比如(a,b,c,d)的深度为1,比如(a,(b,c),d)的深度为2
- 串是内容受限的线性表,它限定了表中的元素为字符。
- 多维数组可以看成是线性表的推广,其特点是结构中的元素本身可以是具有某种结构的数据,但属于同一数据类型。
- 广义表是另一种线性表的推广形式,表中的元素可以是称为原子的单个元素,也可以是一个子表,所以线性表可以看成广义表的特例。
特殊矩阵:
- 特殊矩阵:值相同的元素或者零元素在矩阵中的分布有一定规律。
对称矩阵
满足:A[i][j] == A[j][i]例子(主对角线两边对称):
A =
[ 1 2 3 ]
[ 2 4 5 ]
[ 3 5 6 ]A[0][1] = 2与A[1][0] = 2相等,其他同理。- 主对角线为对称轴。
上三角矩阵(上半区有值,下半为0):
U =
[ 1 2 3 ]
[ 0 4 5 ]
[ 0 0 6 ]下三角矩阵(下半区有值,上半为0):
L =
[ 1 0 0 ]
[ 2 4 0 ]
[ 3 5 6 ]- 主对角线下/上方全部为 0 或固定值,常见于高斯消元等场景。
对角矩阵(Diagonal Matrix)
例子(除主对角线外全为 0):
D =
[ 1 0 0 ]
[ 0 2 0 ]
[ 0 0 3 ]- 只有
A[0][0],A[1][1],A[2][2]非 0,其他为 0。 - 带状矩阵是对角矩阵的推广,例如:
带状对角矩阵(主对角线和其上下各一条对角线也有值):
B =
[ 1 2 0 ]
[ 3 4 5 ]
[ 0 6 7 ]稀疏矩阵:
- 稀疏矩阵:其非零元素较零元素少,且分布没有一定规律
- 存储方法:
三元组表
用一个三元组 (row, col, value) 来表示一个非零元素的位置和数值,节省空间。
稀疏矩阵 ➜ 用三元组 ➜ 每个非零值 ➜ 一个记录 (i, j, v)
原始稀疏矩阵:
M =
[ 0 0 3 ]
[ 4 0 0 ]
[ 0 5 0 ]三元组表示为:
(row, col, value)
(0, 2, 3)
(1, 0, 4)
(2, 1, 5)好处:只记录非零元素,空间效率高。
十字链表法
为每行每列建立指针,将非零元素用结点连接,适合频繁插入删除。
- 每个非零节点包含:值、行下标、列下标、右指针、下指针
- 每行有一个行头结点,每列有一个列头结点
稀疏矩阵 ➜ 链表 ➜ 横指针右移(行)、竖指针下移(列)
稀疏矩阵:
M =
[ 0 0 3 ]
[ 4 0 0 ]
[ 0 5 0 ]十字链表中节点内容为(每个节点):
(0,2,3)→ 行0的右指针指向它,列2的下指针指向它(1,0,4)→ 行1的右指针,列0的下指针(2,1,5)→ 行2的右指针,列1的下指针
好处:
- 插入删除快
- 遍历某行或某列效率高
- 空间效率适中,比三元组表更适合动态变化的数据结构
广义表
| 项目 | 含义描述 | 例子 |
|---|---|---|
| 长度 | 广义表最外层元素的个数 | (a, b, (c, d), e) 长度为 4 |
| 深度 | 广义表中括号嵌套的最大层数 | (a, (b, (c, d))) 深度为 3 |
| 表头 | 第一个元素(不管是原子还是子表) | (a, b, c) 的表头为 a |
| 表尾 | 除去第一个元素后的剩余部分(仍然是广义表) | (a, b, c) 的表尾为 (b, c) |
树和二叉树
概念
| 速记点编号 | 名称 | 定义说明 | 示例(以下图树为例) |
|---|---|---|---|
| 1️⃣ | 子节点 / 孩子节点 | 某节点直接连接的下一层节点 | A 的子节点有 B、C、D |
| 2️⃣ | 节点的度 | 某节点的子节点数 | A 的度是 3;B 的度是 2 |
| 3️⃣ | 叶节点 / 终端节点 | 度为 0 的节点(没有子节点) | E、F、G、H 是叶节点 |
| 4️⃣ | 非终端节点 | 度不为 0 的节点 | A、B、C 是非终端节点 |
| 5️⃣ | 父节点 / 双亲节点 | 某节点的直接上层节点 | B 的父节点是 A,E 的父节点是 B |
| 6️⃣ | 兄弟节点 | 具有相同父节点的节点 | B、C、D 是兄弟节点;E 和 F 是兄弟 |
| 7️⃣ | 树的度 | 树中所有节点度的最大值 | 树的度是 3(A 有 3 个子节点) |
| 8️⃣ | 节点的层次 | 根为第 1 层,子节点为第 2 层,以此类推 | A 在第 1 层,B 在第 2 层,E 在第 3 层 |
| 9️⃣ | 树的高度 / 深度 | 节点的最大层次 | 最深为第 3 层,所以高度是 3 |
| 🔟 | 堂兄弟节点 | 父节点不同,但父节点在同一层的节点 | E(父为 B)和 G(父为 C)是堂兄弟 |
| 1️⃣1️⃣ | 祖先节点 | 从根到某节点路径中经过的所有节点 | E 的祖先有 A 和 B |
| 1️⃣2️⃣ | 子孙节点 | 某节点为根的子树中所有节点 | B 的子孙包括 E 和 F |
A
/ | \
B C D
/ \ \
E F G
\
H树的表示方法
| 表示方法 | 描述说明 |
|---|---|
| 树形表示法 | 以树的结构展示节点之间的层次关系,直观易懂 |
| 嵌套集合表示法 | 使用集合嵌套的方式表示树的层次结构 |
| 凹入表示法 | 通过缩进表示节点的层次关系,层次越深缩进越多 |
| 广义表表示法 | 使用广义表的形式表示树的结构,类似于列表嵌套 |
树形表示法
A
/ | \
B C D
/ \ \
E F G
\
H嵌套集合表示法
{A, {B, {E}, {F}}, {C, {G, {H}}}, {D}}凹入表示法
A
B
E
F
C
G
H
D广义表表示法
(A, (B, (E, F)), (C, (G, H)), D)树的存储结构
| 存储方式 | 结构特点 |
|---|---|
| 双亲顺序存储结构 | 每个节点包含数据和其父节点在数组中的下标。适用于查找双亲操作多的场景。 |
| 孩子链式存储结构 | 每个节点有一个指针域,指向其“所有子节点的链表头”。适合查找子节点频繁的场景。 |
| 孩子兄弟存储结构 | 每个节点有两个指针:一个指向第一个孩子,一个指向下一个兄弟。适合任意树转二叉树。 |
双亲顺序存储结构
A
/ | \
B C D
/ \ \
E F G
\
H孩子链式存储结构
A
/ | \
B C D
/ \ \
E F G
\
H孩子兄弟存储结构
A
/ | \
B C D
/ \ \
E F G
\
H二叉树
- 满二叉树:深度为 k,有 2^k-1 个结点
- 完全二叉树:深度为 k,有 n 个结点,且结点 1 到 k-1 是满二叉树,第 k 层从左到右依次填充
- 满二叉树一定是完全二叉树,但完全二叉树不一定是满二叉树
这个是满二叉树,也是完全二叉树
1
/ \
2 3
/ \ / \
4 5 6 7| 性质内容 | 示例(以 n = 7 的完全二叉树为例) |
|---|---|
| 深度为 k 的二叉树最多有 2^k - 1 个节点 | 深度为 3 时最多节点数:2³ - 1 = 7 |
| 叶子结点数 n_0 = n_2 + 1,其中 n_2 是度为 2 的结点数 | 若有 3 个度为 2 的节点,则叶子结点数为 3 + 1 = 4 |
| n 个节点的完全二叉树深度是 ⌊log₂n⌋ + 1 | n=7,⌊log₂7⌋ + 1 = 2 + 1 = 3 层 |
| 第 i 个结点的双亲编号为 ⌊i/2⌋(i=1 时无父节点) | 编号 3 的节点:⌊3/2⌋ = 1,其父是 1 号节点 |
| 左孩子为编号 2i,若 2i > n,则无左孩子 | 编号 3 的节点:左孩子编号 2×3=6,存在 |
| 右孩子为编号 2i+1,若 2i+1 > n,则无右孩子 | 编号 3 的节点:右孩子编号 2×3+1=7,存在 |
| 对任何一棵二叉树,度为0的结点(叶子结点)总是比度为2的结点多一个 | 叶子结点数为 4,度为2的结点数为 3,叶子结点数比度为2的结点数多1 |
- 节点的编号与其父节点编号之间存在固定的数学关系。对于任意一个编号为n的节点,其父节点的编号为 n/2 (向下取整)
- 二叉树的先序遍历序列和后序遍历序列正好相反,这棵树必须是一条单向的斜线,且树的高度恰好等于结点数。
二叉树的存储结构
| 存储方式 | 描述 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|---|
| 顺序存储结构 | 用数组表示完全二叉树,节点编号从 1 开始,节点 i 的左孩子是 2i,右孩子是 2i+1 | 快速定位父子节点 | 空间浪费(非完全二叉树) | 完全二叉树或接近完全 |
| 链式存储结构 | 每个节点用一个结构体(或对象)表示,含数据域、左孩子指针、右孩子指针 | 空间利用率高,灵活 | 不能随机访问 | 一般二叉树 |
二叉树的遍历
- 中序遍历专属于二叉树,因为它需要左右子树的明确划分,其他树形结构没有这种区分,所以不存在中序遍历。
1
/ \
2 3
/ \ / \
4 5 6 7| 遍历方式 | 顺序规则 | 遍历结果 | 口诀 |
|---|---|---|---|
| 前序遍历 | 根 → 左 → 右 | 1 2 4 5 3 6 7 | 根在前 |
| 中序遍历 | 左 → 根 → 右 | 4 2 5 1 6 3 7 | 根在中 |
| 后序遍历 | 左 → 右 → 根 | 4 5 2 6 7 3 1 | 根在后 |
| 层次遍历 | 按层从左到右 | 1 2 3 4 5 6 7 | BFS |
树和森林遍历
- 森林:多棵树组成,可先转为二叉树再进行遍历
| 遍历类型 | 访问顺序 | 说明 | 口诀 |
|---|---|---|---|
| 先根遍历 | 根 → 左 → 右 | 先访问根节点,再访问子树(前序遍历) | 根左右 |
| 后根遍历 | 左 → 右 → 根 | 先访问所有子树,最后访问根节点 | 左右根 |
| 层次遍历 | 从上到下,从左到右 | 按层次顺序访问节点,广度优先遍历 | 层次遍历(BFS) |
树1: A
/ \
B C
/
D
树2: X
/ | \
Y Z W- 先根遍历(访问顺序:先遍历树1,再遍历树2):
A B D C X Y Z W- 后根遍历(访问顺序:先遍历树1,再遍历树2):
D B C A Y Z W X- 层次遍历(访问顺序:先遍历树1,再遍历树2):
A B C D X Y Z W森林转换成二叉树
将森林中的每棵小树以“左孩子-右兄弟”方式转换成二叉树结构。
- 例如,假设有一棵树,根节点A有三个子节点B、C、D。转换后,B是A的左孩子,C是B的右兄弟,D是C的右兄弟。
A /|\ B C D 转换为: A / B \ C \ D将第二棵二叉树作为第一棵二叉树的右孩子。
- 举例来说,如果有两棵树,第一棵树的根节点是A,第二棵树的根节点是X,那么转换后,X将作为A的右孩子。
第一棵树: A / B 第二棵树: X / Y 转换为: A / \ B X / Y第三棵二叉树作为第一棵二叉树右孩子的右孩子,以此类推。
- 例如,假设有三棵树,第一棵树的根节点是A,第二棵树的根节点是X,第三棵树的根节点是Y。转换后,X是A的右孩子,Y是X的右孩子。
第一棵树: A / B 第二棵树: X / Y 第三棵树: Z / W 转换为: A / \ B X / \ Y Z / W
赫夫曼树
- Huffman算法:每次选择权值最小的两个节点合并,形成一个新的节点,权值为两个节点权值之和
- 最优二叉树(也称哈夫曼树)中,如果有n个叶子结点,那么一定有n-1个分支结点。这是由最优二叉树的构造特点决定的。
| 速记点 | 定义 | 举例 |
|---|---|---|
| 树的路径长度 | 所有结点从根到该结点路径长度的总和。完全二叉树路径长度最短。 | 如完全二叉树(3层满二叉树),路径长度最短。 |
| 带权路径长度(WPL) | 所有叶子结点路径长度乘以对应权值的加和。 | 有叶子结点权值分别为2、3、5,路径长度分别为1、2、2,WPL=2×1+3×2+5×2=20 |
| 赫夫曼编码 | 从根开始,左分支编码0,右分支编码1,叶子结点路径编码。 | 权值5的叶子结点路径为“左-右-左”,编码为“0 1 0”。 |
假设一棵树结构如下:
(root)
/ \
A(2) B(3)
/ \
C(5) D(1)路径长度:
- root到A的路径长度 = 1
- root到B的路径长度 = 1
- root到C的路径长度 = 2
- root到D的路径长度 = 2
- 树的路径长度 = 1 + 1 + 2 + 2 = 6
带权路径长度(WPL)(只考虑叶子节点,假设A、C、D是叶子):
- A(权2)路径长度1,贡献 = 2×1=2
- C(权5)路径长度2,贡献 = 5×2=10
- D(权1)路径长度2,贡献 = 1×2=2
- WPL = 2 + 10 + 2 = 14
赫夫曼编码(假设左0右1):
- A的路径是左分支 =
0 - B是右分支 =
1 - C是B的左分支 =
1 0 - D是B的右分支 =
1 1
- A的路径是左分支 =
最优二叉树
- 指的是带权路径长度(WPL)最小的二叉树
- 最常见的最优二叉树就是 —— 赫夫曼树(Huffman Tree)
B树
| 内容 | 备注示例 |
|---|---|
| 所有叶子结点都在同一层 | 没有“高度不一致”问题 |
| M 阶表示最多有 M 个子树指针(即 M 个分支) | M 阶 = 最多 M 个孩子 |
关键字数量满足 ⌈m/2⌉ - 1 ≤ n ≤ m - 1 | 每个结点至少要有一半满 |
| 关键字递增排列 | 支持范围查找 |
B树和B+树对比
| 对比项 | B 树 | B+ 树 |
|---|---|---|
| 用途 | 多用于文件系统索引 | 多用于数据库索引 |
| 子树数 | 有 n 个关键字 → n+1 棵子树 | 有 n 个关键字 → n 棵子树 |
| 数据存储 | 数据存储在所有结点上(内结点 + 叶结点) | 数据只存在叶子节点,内节点只作索引 |
| 查询效率 | 查询速度中等,可能在内结点找到 | 所有查找都到叶子,查找路径一致,适合范围查询 |
| 叶子节点链接 | 不一定有链接 | 所有叶子结点通过指针串联,便于区间遍历 |
图
- 线性表可以是空表,树可以是空树,但图不可以是空图
概念
- 无向图∶每条边都是没有方向的
- 有向图∶每条边都是有方向的
- 连通图:图中任意两个顶点都是连通的(有路径的)
- 顶点度数:
- 无向图:顶点v的度数是与v相关联的边的数目
- 有向图:顶点v的度数是顶点v的入度(该顶点为终点的边的数目)与出度(以该顶点为起点的边的数目)之和
- 连通分量:无向图中的极大连通子图
- 连通子图:内部任意两个顶点都连通。
- 极大(最大):不能再往里加点使它仍然连通了,一旦加点就“不全连通”了。
- 强连通图:有向图中任意两个顶点都是连通的
A → B
↑ ↓
D ← C- 强连通分量:有向图中的极大强连通子图
图的存储结构
- 邻接矩阵:所谓邻接矩阵存储,是指用一个一维数组存储图中顶点的信息,用一个二维数组存储图中边的信息(即各顶点之间的邻接关系),存储顶点之间邻接关系的二维数组称为邻接矩阵。
- 邻接表:在邻接表中存在两种结点:顶点表结点和边表结点
- 十字链表:十字链表是有向图的一种链式存储结构。在十字链表中,对应于有向图中的每条弧有一个结点,对应于每个顶点也有一个结点。
- 邻接多表:邻接多重表是无向图的另一种链式存储结构。
邻接矩阵
| 图类型 | 行/列意义 | 特点 | 边数与1的关系 | 空间优化 |
|---|---|---|---|---|
| 有向图 | 行:出度,列:入度 | 入度和 = 出度和 | 所有 1 的个数 = 边数 | 无法压缩 |
| 无向图 | 行或列的 1 的个数 = 顶点度 | 矩阵对称 | 所有 1 的个数 = 边数 × 2 | 可压缩为上/下三角区域 |
定义:邻接矩阵由两个部分组成:
- 顶点数组(存储所有顶点)
- 邻接矩阵(二维数组表示顶点之间的边)
1️⃣ 有向图示例
图结构:
A → B
B → C邻接矩阵(有向):
A B C
-------
A | 0 1 0
B | 0 0 1
C | 0 0 0出度:
- A 的出度 = 第 1 行中 1 的个数 = 1
- B 的出度 = 第 2 行中 1 的个数 = 1
- C 的出度 = 第 3 行中 1 的个数 = 0
入度:
- A 的入度 = 第 1 列中 1 的个数 = 0
- B 的入度 = 第 2 列中 1 的个数 = 1
- C 的入度 = 第 3 列中 1 的个数 = 1
总出度 = 总入度 = 2 ✅
2️⃣ 无向图示例
图结构:
A — B
B — C邻接矩阵(无向):
A B C
-------
A | 0 1 0
B | 1 0 1
C | 0 1 0- 对称矩阵 ✅
- A 度 = 第 1 行中 1 的个数 = 1
- B 度 = 第 2 行中 1 的个数 = 2
- C 度 = 第 3 行中 1 的个数 = 1
矩阵中总共有 4 个 1,对应 2 条边(因为每条边占两个 1)✅
- 对称矩阵 ➜ 只需存上三角或下三角部分(不含对角线)
- 空间需求 = n(n - 1)/2
比如:
- 对于 5 个顶点,需空间 = 5×4/2 = 10 个元素
邻接表
| 描述 | 备注举例 |
|---|---|
| 定义:对图中每个顶点都建立一个单链表,存储该顶点的邻接点信息。 | 每个顶点对应一个链表,链表节点为邻接点 |
| 无向图中,某顶点的邻接表节点数 = 该顶点的度(与多少个顶点相连)。 | 顶点 A 与 B、C 相连,A 的邻接表有 2 个节点 |
| 有向图中,某顶点的邻接表节点数 = 该顶点的出度(指向多少个顶点)。 | 顶点 A 有边指向 B、C,A 的邻接表有 2 个节点 |
简单示例
无向图:顶点 A — B、C 邻接表:
A -> B -> C B -> A C -> A有向图:顶点 A → B、C 邻接表:
A -> B -> C B -> (无邻接点) C -> (无邻接点)
邻接矩阵和邻接表对比
| 特性 | 邻接矩阵 | 邻接表 |
|---|---|---|
| 定义 | 用二维数组存储顶点间边的关系 | 用链表存储每个顶点的邻接点信息 |
| 空间复杂度 | 固定为 $O(n^2)$ | 边少时节省空间,约为 $O(n + e)$ |
| 适用场景 | 边数多,稠密图 | 边数少,稀疏图 |
| 查询边是否存在 | $O(1)$ 直接通过矩阵索引查找 | 需要遍历链表,最坏 $O(k)$ (k是度) |
| 遍历邻接点 | 需扫描整行,时间 $O(n)$ | 直接遍历链表,时间 $O(k)$ |
| 入度/出度统计 | 有向图:行代表出度,列代表入度,易统计 | 出度易统计,入度不易,需遍历所有链表 |
| 实现复杂度 | 简单,数组直接实现 | 较复杂,需要链表指针操作 |
十字链表
邻接多表
图的遍历
| 内容 | DFS(深度优先遍历) | BFS(广度优先遍历) |
|---|---|---|
| 遍历方式 | 类似树的先序遍历,从一个顶点沿深度方向尽可能走远 | 类似树的层次遍历,一层层按广度逐层访问 |
| 适用图类型 | 有向图或无向图均可 | 有向图或无向图均可 |
| 数据结构实现 | 栈(递归调用本质上用栈) | 队列 |
| 应用场景 | 路径搜索、拓扑排序、连通性检测 | 最短路径搜索(无权图)、层次划分 |
| 访问顺序特点 | 先访问尽可能深的邻接点,后回溯 | 先访问当前层所有邻接点,再访问下一层 |
最小生成树
- 保留 n - 1 条边,其中 n 是顶点数
- 所有顶点都连通(连通图)
- 边权和最小
- 没有环(是树结构)
- 在带权无向连通图中,选出一棵包含所有顶点的生成树,使所有边权之和最小。
最小生成树算法
| 特点 | Prim 算法 | Kruskal 算法 |
|---|---|---|
| 思路 | 顶点为中心,逐渐扩展生成树 | 边为中心,按权值排序选择边 |
| 适用图类型 | 稠密图更优 | 稀疏图更优 |
| 数据结构 | 通常使用优先队列(堆)维护边 | 并查集(Union-Find)判环 |
| 操作步骤 | 每次选取与生成树相连的最小边 | 按边权从小到大加入边,避免环路 |
| 时间复杂度 | $O(V^2)$ 或 $O(E \log V)$(堆优化) | $O(E \log E)$(排序边和并查集) |
| 举例 | 从起点A开始,逐渐连入权重最小的边 | 从最小边开始,连通不同集合的顶点 |
简单例子:
图的顶点和边(权重):
顶点:A, B, C
边:
A — B : 1
B — C : 2
A — C : 3图示:
A — 1 — B
\ |
3 2
\ /
CPrim 算法(从 A 开始):
- 起点 A,只连接 A-B(1) 和 A-C(3),选最小边 A-B(1)
- 集合
- 连接 B-C(2) 和 A-C(3),选 B-C(2)
- 集合 {A, B, C},结束
选边:A-B(1), B-C(2)
Kruskal 算法:
按权重排序边:A-B(1), B-C(2), A-C(3)
依次加入边,不成环:
- 加 A-B(1)
- 加 B-C(2)
- 加 A-C(3) 会成环,跳过
选边:A-B(1), B-C(2)
最小生成树边集:
A-B (1), B-C (2)总权重:
1 + 2 = 3拓扑排序
- 应用于有向无环图(DAG),不适用有环图。
- 排序结果是一种满足依赖关系的线性序列。
- 常用于任务调度、编译依赖分析等场景。
拓扑排序算法
| 特点 | AOV网 | AOE网 |
|---|---|---|
| 图的元素 | 顶点是活动,弧是顺序关系 | 顶点是事件,弧是活动(带时间) |
| 主要用途 | 分析活动依赖顺序 | 关键路径分析、时间管理 |
AOV网(Activity on Vertex)
- 顶点表示活动,边表示活动间的依赖关系。
例子:
活动:A, B, C, D
依赖关系:
- A → C (完成A后才能开始C)
- B → C
- C → D
图示(顶点是活动):
A B
\ /
C
|
DAOE网(Activity on Edge)
- 顶点表示事件(活动的开始或结束时刻),边表示活动,边上带活动持续时间。
例子:
事件:1, 2, 3, 4
活动及持续时间:
- 活动A(持续3天):1 → 2
- 活动B(持续2天):1 → 3
- 活动C(持续4天):2 → 4
- 活动D(持续5天):3 → 4
图示(边是活动):
1
|\
| \
A B
(3)(2)
| \
2-----3
\ \
C D
(4) (5)
\ /
4最短路径算法
| 特点 | 迪杰斯特拉算法(Dijkstra) | 弗洛伊德算法(Floyd) |
|---|---|---|
| 计算目标 | 单源最短路径 | 所有顶点对最短路径 |
| 支持的权值类型 | 非负权边 | 可含负权边(无负权回路) |
| 时间复杂度 | $O((V+E) \log V)$(使用堆优化) | $O(V^3)$ |
| 算法思想 | 贪心 | 动态规划 |
| 适用图类型 | 稠密或稀疏图 | 较小规模图 |
| 典型应用 | 地图导航、网络路由 | 交通网络全局路径规划 |
举例
图的顶点和边(带权有向图)
顶点:A, B, C, D
边及权重:
A → B : 1
A → C : 4
B → C : 2
B → D : 6
C → D : 3Dijkstra 算法(单源最短路径)
目标:
从顶点 A 出发,找出 A 到其他顶点的最短路径。
过程:
| 步骤 | 确定的最短路径 | 距离估计 (A 到各点) |
|---|---|---|
| 初始化 | A到A距离0,其他∞ | A:0, B:∞, C:∞, D:∞ |
| 1 | 从A开始,更新邻接点距离 | B:1 (A→B), C:4 (A→C), D:∞ |
| 2 | 选择未确定中距离最小点B(距离1) | 通过B更新C和D:C:3 (1+2), D:7 (1+6) |
| 3 | 选择未确定中距离最小点C(距离3) | 通过C更新D:D:6 (3+3) |
| 4 | 选择未确定中距离最小点D(距离6) | 结束 |
结果:
- A→A: 0
- A→B: 1
- A→C: 3
- A→D: 6
Floyd 算法(所有顶点对最短路径)
目标:
计算任意两点间的最短路径。
初始化邻接矩阵(无连接为 ∞):
| A | B | C | D | |
|---|---|---|---|---|
| A | 0 | 1 | 4 | ∞ |
| B | ∞ | 0 | 2 | 6 |
| C | ∞ | ∞ | 0 | 3 |
| D | ∞ | ∞ | ∞ | 0 |
过程:
动态更新路径长度,尝试通过顶点 k(从 A 到 D)中转。
- 以 k=A,k=B,k=C,k=D 为中转点,更新路径长度。
- 最终邻接矩阵:
| A | B | C | D | |
|---|---|---|---|---|
| A | 0 | 1 | 3 | 6 |
| B | ∞ | 0 | 2 | 5 |
| C | ∞ | ∞ | 0 | 3 |
| D | ∞ | ∞ | ∞ | 0 |
总结
- Dijkstra:从A点出发,找出到其他点的最短路径。
- Floyd:计算所有点之间的最短路径。
查找
概念
| 速记点 | 静态查找表 | 动态查找表 |
|---|---|---|
| 定义 | 只能进行查找操作的查找结构 | 在查找过程中可以同时进行插入和删除操作 |
| 数据元素 | 固定不变,表内数据元素不增删 | 支持元素的动态增删,表内容可变化 |
| 典型应用 | 只读的数据集合,如词典、配置文件 | 实时更新的数据集合,如数据库索引、缓存 |
| 维护复杂度 | 较低,因为数据固定,结构简单 | 较高,需要维护结构平衡或调整以保证效率 |
查找方法
| 方法名称 | 速记内容 | 适用条件 | 特点说明 |
|---|---|---|---|
| 顺序查找法 | 又称线性查找,在无序或有序的线性表中逐个查找 | 适用于无序或有序线性表 | 简单,效率低,时间复杂度O(n) |
| 折半查找法 | 又称二分查找,针对有序顺序表,通过不断折半范围缩小查找范围 | 只适用于有序的顺序表 | 高效,时间复杂度O(log n) |
| 分块查找法 | 又称索引顺序查找,结合顺序查找和折半查找优点,分块并建立索引 | 适用于数据量较大且有序的顺序表 | 结构动态,查找速度快 |
BST 二叉搜索树
- 左子树所有节点值小于根节点值
- 右子树所有节点值大于根节点值
- 左右子树也分别为二叉搜索树
平衡二叉树 AVL树
- 左右子树高度差不超过1
- 左右子树也分别为平衡二叉树
| 特点 | AVL树 | 红黑树 |
|---|---|---|
| 定义 | 一种高度平衡的二叉排序树,任意节点左右子树高度差 ≤ 1 | 一种自平衡的二叉搜索树,满足红黑性质保证平衡 |
| 平衡条件 | 节点的左右子树高度差最多为1 | 满足红黑性质(节点颜色和路径黑色节点数规则) |
| 平衡强度 | 比红黑树更严格,树更“平” | 平衡条件较松,允许一定不平衡 |
| 旋转次数 | 插入或删除后可能需要多次旋转 | 插入或删除后最多需要两次旋转 |
| 查询效率 | 平均和最坏情况下查询性能好,时间复杂度 $O(\log n)$ | 查询性能略逊于AVL,时间复杂度也为 $O(\log n)$ |
| 插入/删除效率 | 插入删除时调整次数多,开销相对大 | 插入删除时调整次数少,开销相对小 |
| 应用场景 | 适合查询多、修改少的场景 | 适合查询和修改均衡的场景,常用于系统底层数据结构 |
哈希表(散列表)
- 根据关键字 直接计算出地址 进行查找,提高查找效率,平均时间复杂度为 O(1)。
哈希函数构造方法
| 方法名称 | 描述 | 例子(M=13) |
|---|---|---|
| 直接定址法 | f(key) = key | key = 10 → f(10)=10 |
| 除留余数法 | f(key) = key mod M | key = 26 → f(26)=0 |
| 数字分析法 | 从 key 中取出某几位数字作为地址 | key=123456 → 取345 |
| 平方取中法 | 对 key 平方后取中间几位作为地址 | key=123 → 123²=15129 → 取中间512 |
哈希冲突解决方法
| 方法 | 描述 | 举例 |
|---|---|---|
| 开放定址法 | 冲突后向后找下一个空位(线性探测/二次探测) | 位置冲突后试 M+1、M+2... |
| 链地址法 | 每个槽位存一个链表,冲突的 key 依次链入 | 类似“拉链法” |
| 再哈希法 | 换另一个哈希函数再计算地址 | 多函数备用 |
| 建立公共溢出区 | 所有冲突的记录统一存储在溢出区 | 辅助数组 |
排序
概念
- 内部排序∶ 指待排序记录存放在内存中进行的排序过程
- 外部排序∶ 指待排序记录的数量很大,内存一次不能容纳全部记录,在排序过程中尚需对外存进行访问的排序过程,通常采用归并排序法。
- 稳定排序∶ 如果在排序文件中存在多个关键字相同的记录,经过排序后,这些关键字相同的记录之间的前后相对次序保持不变的排序方法
- 不稳定排序∶若具有相同关键字的记录在排序结束后,其前后相对次序发生变化的排序方法
插入排序
直接插入排序
示例序列:[7, 2, 8, 1]
步骤演示:
初始:已排序 [7] | 未排序 [2, 8, 1]
插入2:与7比较 → 插入前面 → [2, 7]
插入8:与7比较 → 插入后面 → [2, 7, 8]
插入1:与8、7、2比较 → 插入最前 → [1, 2, 7, 8]📌 结果:[1, 2, 7, 8]
折半插入排序
示例序列:[6, 4, 9, 3]
步骤演示(与插入排序过程一样,但查找插入位置用折半查找):
初始:已排序 [6] | 未排序 [4, 9, 3]
插入4:
二分查找:在[6]中找4的插入位置 → 插入前面 → [4, 6]
插入9:
二分查找:在[4,6]中找9的插入位置 → 插入后面 → [4, 6, 9]
插入3:
二分查找:在[4,6,9]中找3的插入位置 → 插入最前 → [3, 4, 6, 9]📌 结果:[3, 4, 6, 9]
🔎 差别:查插入位置用折半查找(更快),但元素移动过程一样。
希尔排序
示例序列:[9, 1, 2, 5, 7, 4, 8, 6, 3, 5]
核心思想:按间隔分组,对每组进行插入排序,然后缩小间隔重复
第一步:gap = 5,按间隔5分组
原数组:[9, 1, 2, 5, 7, 4, 8, 6, 3, 5]
索引: 0 1 2 3 4 5 6 7 8 9
分组(间隔5):
组1:[9, 4] → 插入排序 → [4, 9]
组2:[1, 8] → 插入排序 → [1, 8]
组3:[2, 6] → 插入排序 → [2, 6]
组4:[5, 3] → 插入排序 → [3, 5]
组5:[7, 5] → 插入排序 → [5, 7]
重排组合:[4, 1, 2, 3, 5, 9, 8, 6, 5, 7]第二步:gap = 2,按间隔2分组
数组:[4, 1, 2, 3, 5, 9, 8, 6, 5, 7]
分组(间隔2):
组1:[4, 2, 5, 8, 5] → 插入排序 → [2, 4, 5, 5, 8]
组2:[1, 3, 9, 6, 7] → 插入排序 → [1, 3, 6, 7, 9]
重排组合:[2, 1, 4, 3, 5, 6, 5, 7, 8, 9]第三步:gap = 1,整体插入排序
数组:[2, 1, 4, 3, 5, 6, 5, 7, 8, 9]
对每个元素进行插入排序:
插入1到2前 → [1, 2, 4, 3, 5, 6, 5, 7, 8, 9]
插入4到正确位置 → [1, 2, 4, 3, 5, 6, 5, 7, 8, 9]
插入3到正确位置 → [1, 2, 3, 4, 5, 6, 5, 7, 8, 9]
...继续插入排序...📌 结果:[1, 2, 3, 4, 5, 5, 6, 7, 8, 9]
💡 理解要点:
- 希尔排序是插入排序的改进版
- 通过大间隔分组,让元素"跳跃式"移动,减少移动次数
- 逐步缩小间隔,最终变成普通的插入排序
- 比直接插入排序效率更高
选择排序
简单选择排序
示例序列:[5, 3, 1, 4]
步骤演示:
初始:[5, 3, 1, 4]
第1轮:找最小值1,与第1位5交换
[1, 3, 5, 4]
第2轮:从第2位开始,找最小值3,已在正确位置
[1, 3, 5, 4]
第3轮:从第3位开始,找最小值4,与第3位5交换
[1, 3, 4, 5]
第4轮:只剩最后一位,已排序完成
[1, 3, 4, 5]📌 结果:[1, 3, 4, 5]
堆排序
示例序列:[4, 1, 3, 2]
步骤演示:
初始:[4, 1, 3, 2]
1. 建堆(大顶堆):
[4, 1, 3, 2] → [4, 2, 3, 1]
2. 依次取出堆顶元素:
取出4 → [1, 2, 3]
取出3 → [1, 2]
取出2 → [1]
取出1 → []
3. 倒序排列:4, 3, 2, 1📌 结果:[1, 2, 3, 4]
交换排序
冒泡排序
示例序列:[5, 3, 1, 4]
步骤演示:
初始:[5, 3, 1, 4]
第1轮:相邻比较交换
5>3 → [3, 5, 1, 4]
5>1 → [3, 1, 5, 4]
5>4 → [3, 1, 4, 5]
第2轮:继续相邻比较
3>1 → [1, 3, 4, 5]
3<4 → [1, 3, 4, 5]
4<5 → [1, 3, 4, 5]
第3轮:继续相邻比较
1<3, 3<4, 4<5 → 无交换,排序完成📌 结果:[1, 3, 4, 5]
快速排序
- 快速排序的主要优势在于处理随机分布的数据,通过分区操作将数据分成两部分进行递归排序。但对于已经接近有序的序列,分区操作的效果很差,导致分区极不均衡。
示例序列:[5, 3, 1, 4]
步骤演示:
初始:[5, 3, 1, 4]
第1轮:选择基准值5
分区:小于5的放左边,大于5的放右边
[3, 1, 4] + [5] + []
递归排序左半部分[3, 1, 4]:
选择基准值3
[1] + [3] + [4]
递归排序右半部分[]:
空数组,无需排序
合并:[1, 3, 4, 5]📌 结果:[1, 3, 4, 5]
归并排序
示例序列:[5, 3, 1, 4]
步骤演示:
初始:[5, 3, 1, 4]
第1层分解:
[5, 3] 和 [1, 4]
第2层分解:
[5] [3] [1] [4]
第1层合并:
[5] + [3] → [3, 5]
[1] + [4] → [1, 4]
第2层合并:
[3, 5] + [1, 4] → [1, 3, 4, 5]📌 结果:[1, 3, 4, 5]
基数排序
示例序列:[23, 12, 31, 45]
步骤演示:
初始:[23, 12, 31, 45]
按个位数排序:
23(3), 12(2), 31(1), 45(5)
→ [31, 12, 23, 45]
按十位数排序:
31(3), 12(1), 23(2), 45(4)
→ [12, 23, 31, 45]📌 结果:[12, 23, 31, 45]
总结
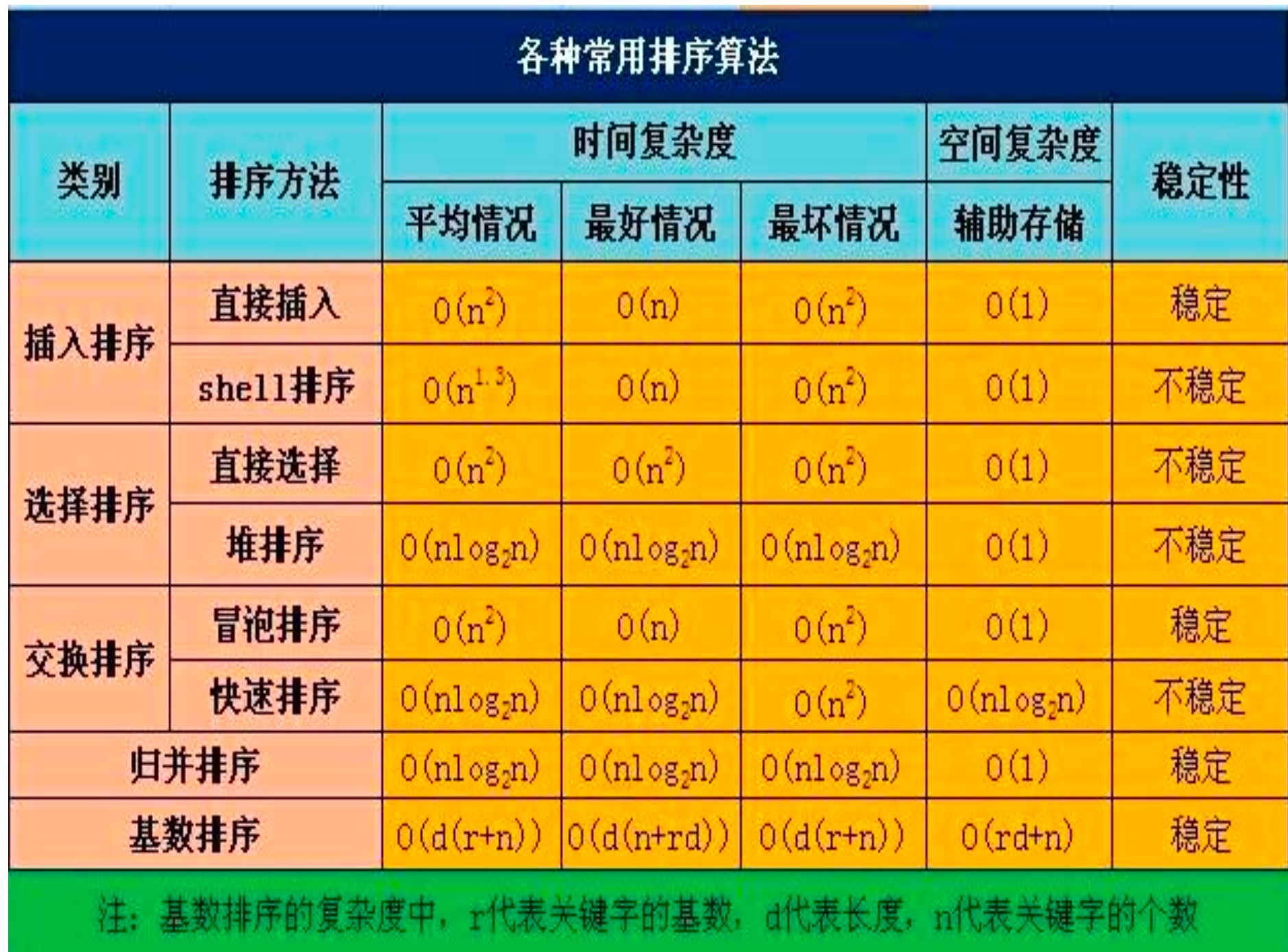
比较次数与初始序列无关的排序方法有哪些?
- 比较次数与初始序列无关的排序方法,主要分为两类:
- 比较类排序:仅选择排序,其比较次数固定为 n(n-1)/2,不随初始序列变化;
- 非比较类排序:以基数排序为代表,无元素间比较操作,自然与初始序列无关(类似的还有计数排序、桶排序,但计数排序依赖 “已知数值范围”,基数排序适用性更广)。
